Fourier demos

Fourier analysis plays a very important role in mathematics. A very short and basic introduction is provided in my Fourier refresher (PDF) handout.

Sums of sine functions can be used to generate quite complicated waveforms. You can try adding two sines and vary the frequencies and amplitudes in the CDF demo below. Note, however, that because the sine function is an "odd" function, i.e. sin(-x) = -sin(x), and because sums of odd functions are also odd, one can decompose only odd functions into a (possibly infinite) sum of sines.

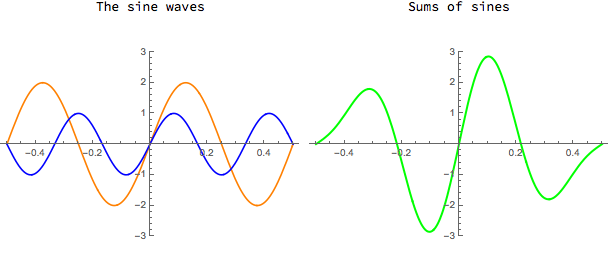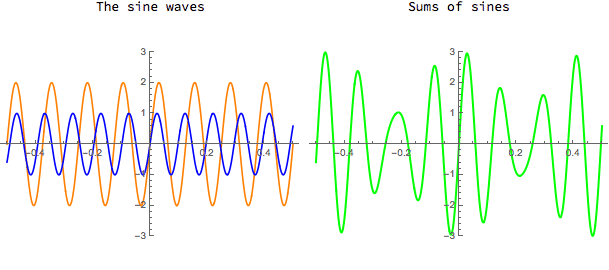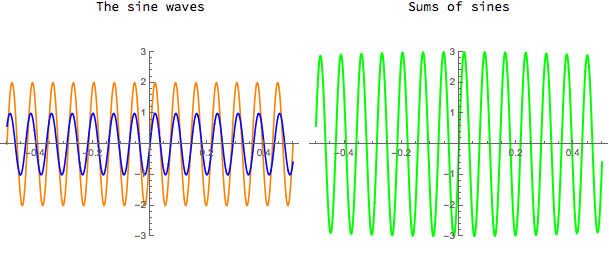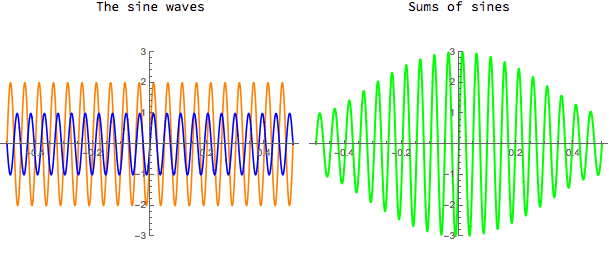
Download CDF

Because the cosine function is "even", i.e. cos(-x) = cos(x), a sum of a sine and a cosine function will be neither even nor odd in general. A big sum of sines and cosines with different amplitudes and frequencies will probably be flexible enough to approximate a large variety of periodic functions.

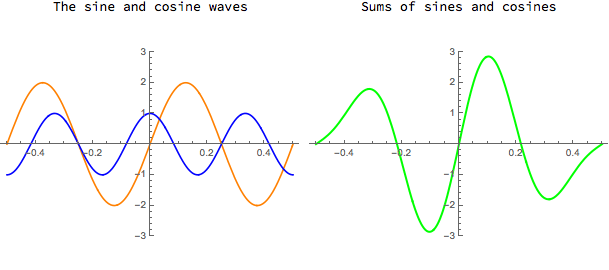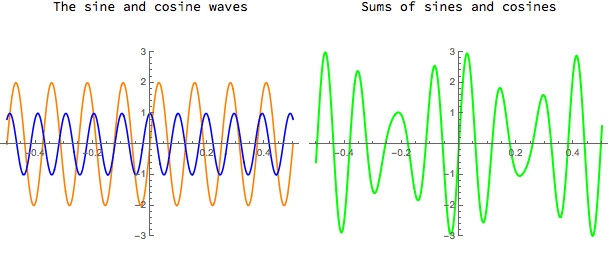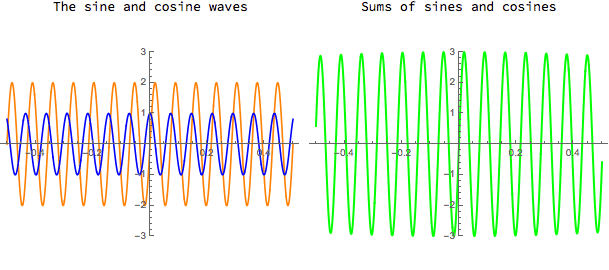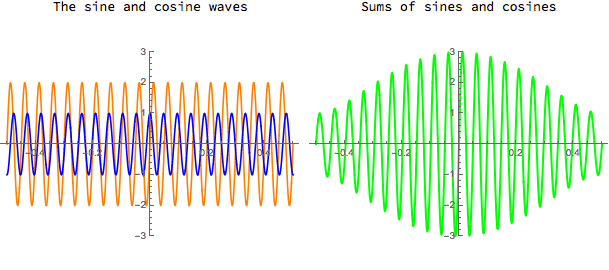
Download CDF

Functions can be approximated by their Fourier series. We try this with the "unit box" function

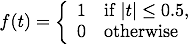
in blue, and its n-th order Fourier series approximation

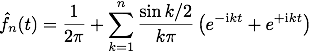
in orange:

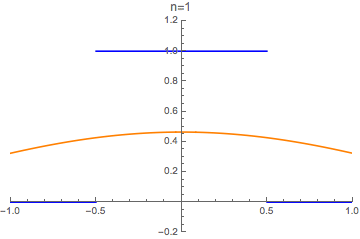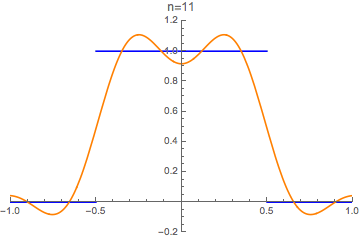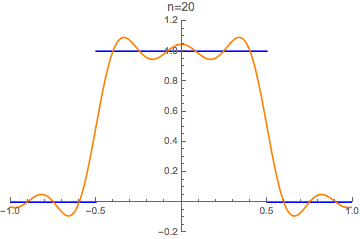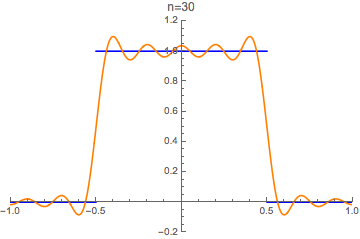
Download CDF